The function ode
provides solvers for systems of ordinary differential equations of the
type:
\[ \frac{dy}{dt} = f(t,y), \quad y(t_0)=y_0 \]
where \(y\) is the vector of state
variables. Two solvers are available: the simpler and faster Euler
scheme1
or the more accurate 4-th order Runge-Kutta method2. Although many
packages already exist to solve ordinary differential equations in R3, they
usually represent the function \(f\)
either with an R function or with characters.
While the representation via R functions is usually more
efficient, the symbolic representation is easier to adopt for beginners
and more flexible for advanced users to handle systems that might have
been generated via symbolic programming. The function ode
supports both the representations and uses hashed
environments to improve symbolic evaluations.
Examples
The vector-valued function \(f\)
representing the system can be specified as a vector of
characters, or a function returning a numeric
vector, giving the values of the derivatives at time \(t\). The initial conditions are set with
the argument var and the time variable can be specified
with timevar.
Symbolic system
\[ \frac{dx}{dt}=x, \quad x_0 = 1 \]
f <- "x"
var <- c(x=1)
times <- seq(0, 2*pi, by=0.001)
x <- ode(f = f, var = var, times = times)
plot(times, x, type = "l")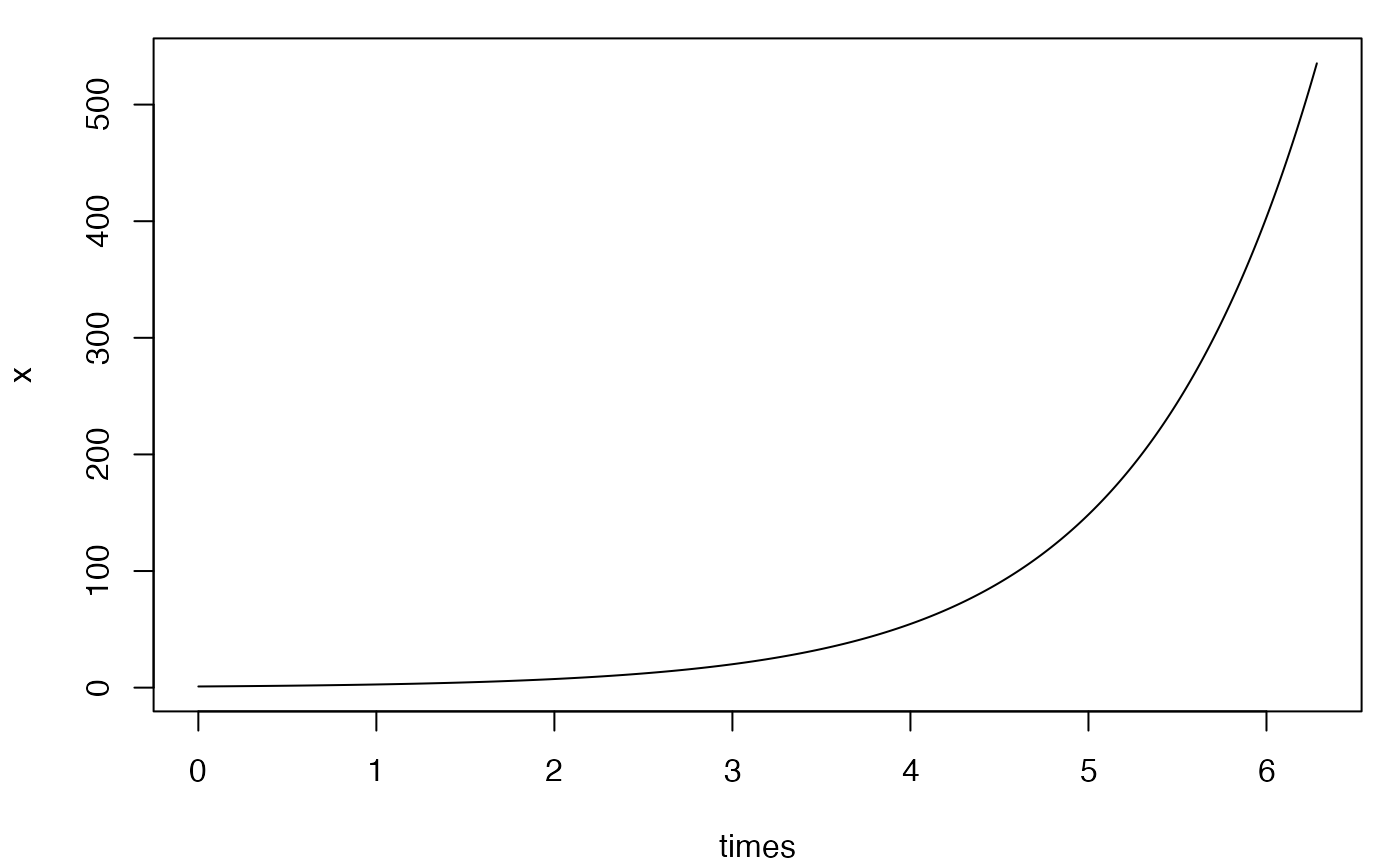
Time dependent system
\[ \frac{dx}{dt}=\cos(t), \quad x_0 = 0 \]
f <- "cos(t)"
var <- c(x=0)
times <- seq(0, 2*pi, by=0.001)
x <- ode(f = f, var = var, times = times, timevar = "t")
plot(times, x, type = "l")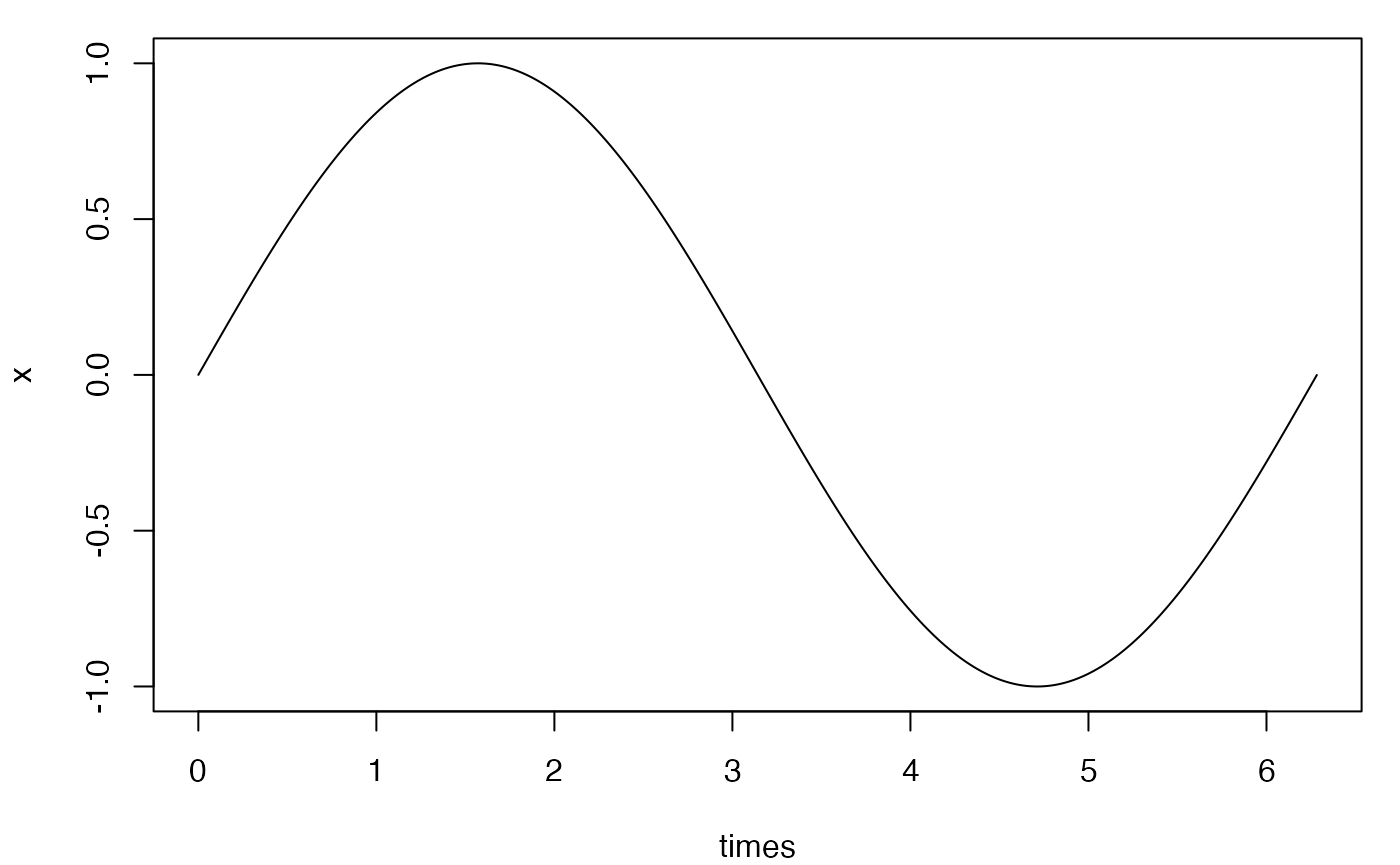
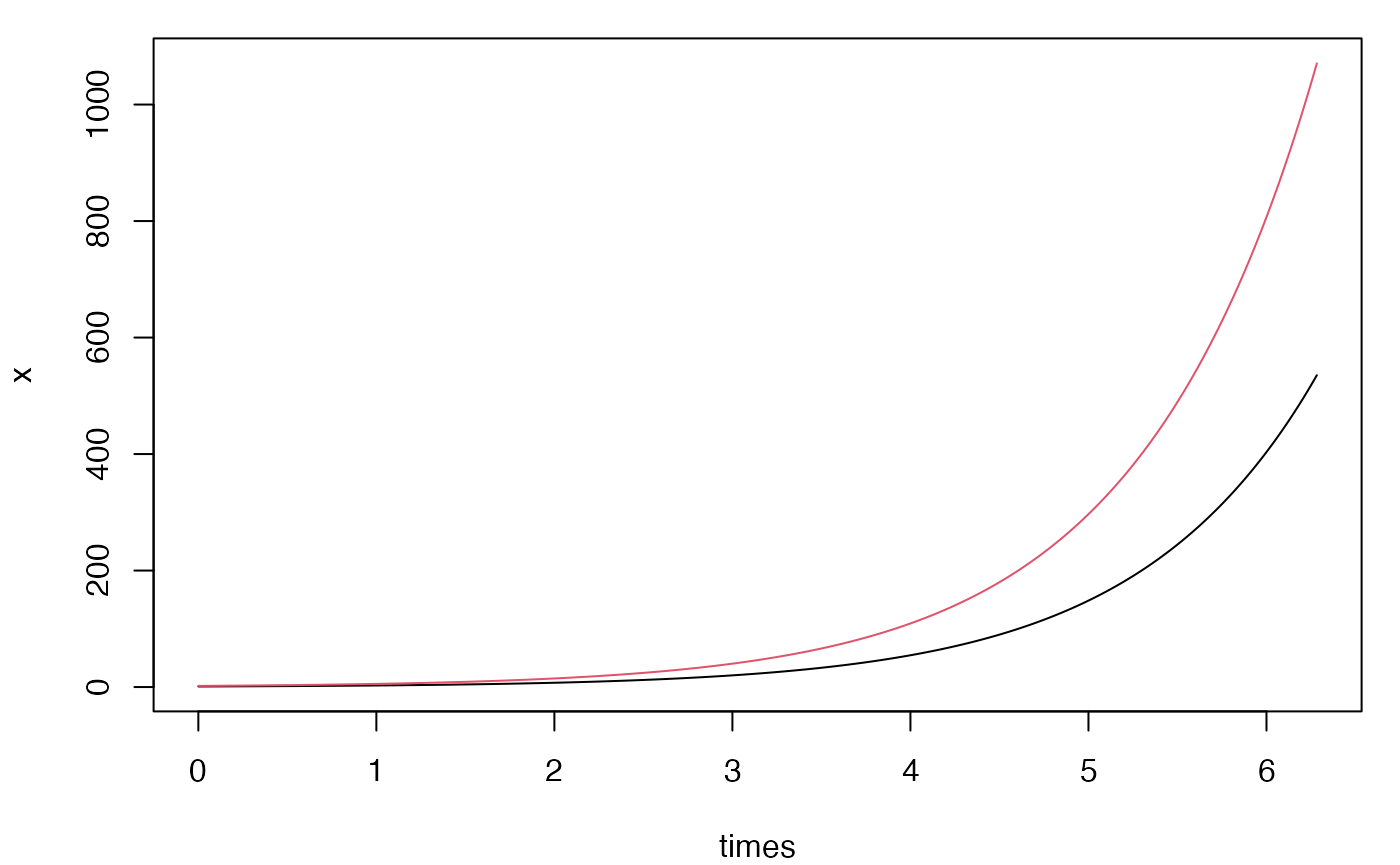
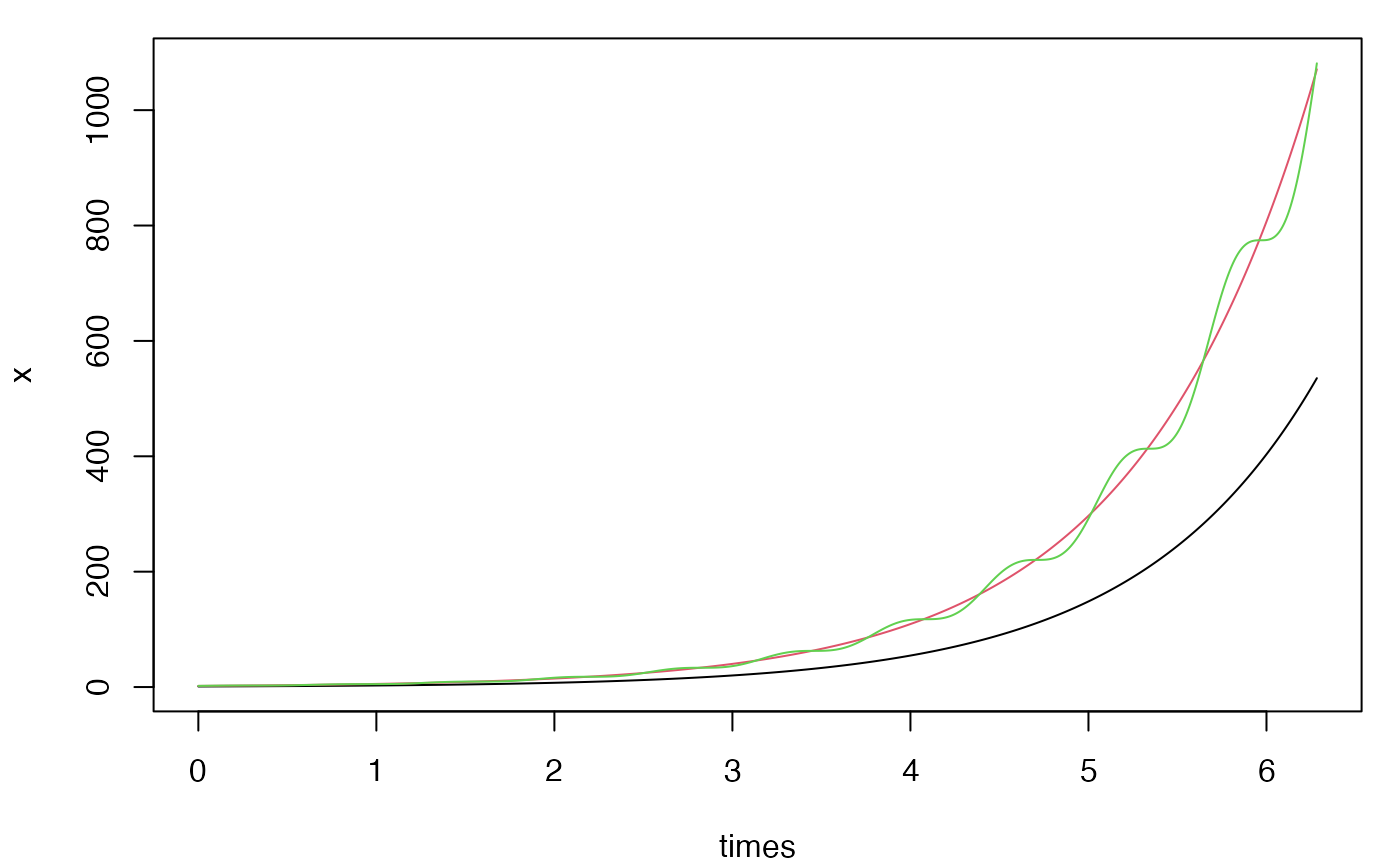
Multivariate system
\[ \frac{d}{dt} \begin{bmatrix} x\\ y \end{bmatrix}= \begin{bmatrix} x\\ x(1+\cos(10t)) \end{bmatrix}, \quad \begin{bmatrix} x_0\\y_0 \end{bmatrix}= \begin{bmatrix} 1\\1 \end{bmatrix} \]
f <- c("x", "x*(1+cos(10*t))")
var <- c(x=1, y=1)
times <- seq(0, 2*pi, by=0.001)
x <- ode(f = f, var = var, times = times, timevar = "t")
matplot(times, x, type = "l", lty = 1, col = 1:2)
Numerical system
\[ \frac{d}{dt} \begin{bmatrix} x\\ y \end{bmatrix}= \begin{bmatrix} x\\ y \end{bmatrix}, \quad \begin{bmatrix} x_0\\y_0 \end{bmatrix}= \begin{bmatrix} 1\\2 \end{bmatrix} \]
f <- function(x, y) c(x, y)
var <- c(x=1, y=2)
times <- seq(0, 2*pi, by=0.001)
x <- ode(f = f, var = var, times = times)
matplot(times, x, type = "l", lty = 1, col = 1:2)
Vectorized interface
\[ \frac{d}{dt} \begin{bmatrix} x\\ y\\ z \end{bmatrix}= \begin{bmatrix} x\\ y\\ y*(1+cos(10*t)) \end{bmatrix}, \quad \begin{bmatrix} x_0\\y_0\\z_0 \end{bmatrix}= \begin{bmatrix} 1\\2\\2 \end{bmatrix} \]
f <- function(x, t) c(x[1], x[2], x[2]*(1+cos(10*t)))
var <- c(1,2,2)
times <- seq(0, 2*pi, by=0.001)
x <- ode(f = f, var = var, times = times, timevar = "t")
matplot(times, x, type = "l", lty = 1, col = 1:3)
Cite as
Guidotti E (2022). “calculus: High-Dimensional Numerical and Symbolic Calculus in R.” Journal of Statistical Software, 104(5), 1-37. doi:10.18637/jss.v104.i05
A BibTeX entry for LaTeX users is
@Article{calculus,
title = {{calculus}: High-Dimensional Numerical and Symbolic Calculus in {R}},
author = {Emanuele Guidotti},
journal = {Journal of Statistical Software},
year = {2022},
volume = {104},
number = {5},
pages = {1--37},
doi = {10.18637/jss.v104.i05},
}